Problem 4.3: Statistics of random genetic circuits
This problem is still a draft.
In the chapter, we discussed in words an algorithm for generating random directed graphs representing interactions among genes. Starting from a set of nodes and directed edges (arrows), we enforce that each node has the same number of incoming and outgoing arrows. It is a fun (and challenging!) problem to implement such an algorithm, which is what you will do in this problem.
We showed that the directed graph can be pictorially represented as a set of nodes with arrows, or as an asymmetric matrix of ones and zeros. Alternatively, and more compactly, it may be represented as an array of 2-tuples, with each 2-tuple representing an arrow connecting two numbered nodes. As an example (8, 2) represents an arrow going from node 8 to node 2, and (10, 11) represents an arrow going from node 10 to node 11.
a) Write a function that takes as input an array of 2-tuples representing the regulatory connections of numbered genes and returns an array of 2-tuples representing a random directed graph in which each node (gene) has the same number of incoming and outgoing arrows as in that input network.
b) Write another function that takes as input an array of 2-tuples representing a network and an array of 2-tuples representing a specific regulatory architecture and then returns the number of instances of that architecture in the input network. Here are some example architectures.
Simple regulation:
[(1, 2)]Mutual regulation (as in a toggle circuit):
[(1, 2), (2, 1)].FFL:
[(1, 2), (1, 3), (2, 3)]
c) Play with your functions with sample circuits. For starters, you can use the example circuit of Milo, et al., shown below,
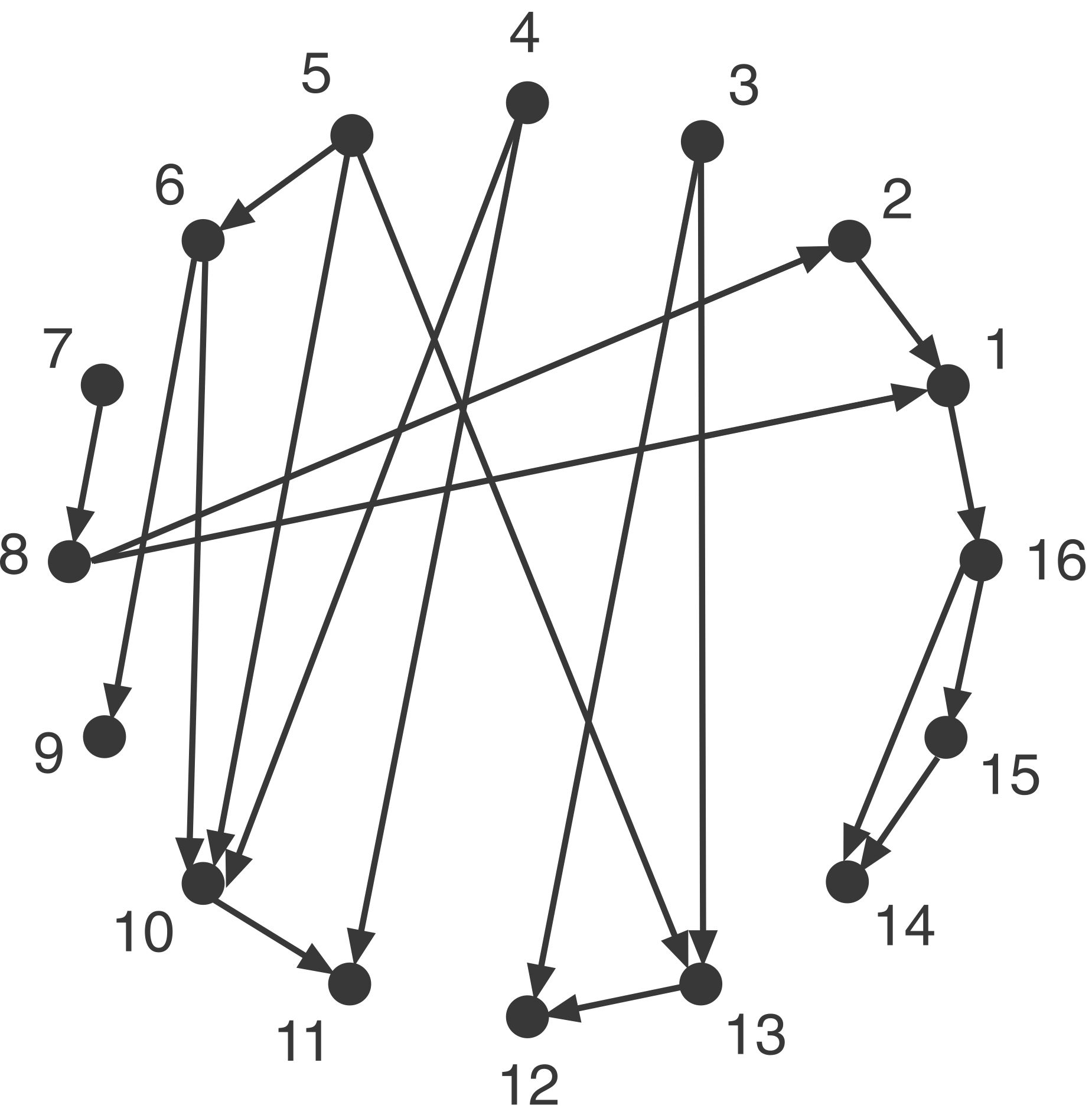
which can be represented as
milo_example_network = [
(1, 16),
(2, 1),
(3, 12),
(3, 13),
(4, 10),
(4, 11),
(5, 6),
(5, 10),
(5, 13),
(6, 9),
(6, 10),
(7, 8),
(8, 1),
(8, 2),
(10, 11),
(13, 12),
(15, 14),
(16, 14),
(16, 15),
]
Try searching for FFLs.