10. Uses, simplifications, and elaborations of negative feedback oscillators
Design principles
Ultrasensitive delayed repression produces oscillations in gene expression.
Combination of delayed negative feedback with positive feedback enables independent tuning of oscillator period and amplitude.
Techniques
Linear stability analysis of delay differential equations (DDEs)
“Brute force” linear stability diagrams
Numerical solution of DDEs
[1]:
# Colab setup ------------------
import os, sys, subprocess
if "google.colab" in sys.modules:
cmd = "pip install --upgrade watermark"
process = subprocess.Popen(cmd.split(), stdout=subprocess.PIPE, stderr=subprocess.PIPE)
stdout, stderr = process.communicate()
# ------------------------------
import numpy as np
import scipy.optimize
import biocircuits
import bokeh.io
import bokeh.plotting
bokeh.io.output_notebook()
We continue our discussion of oscillators by considering a very simple oscillator, even simpler than the repressilator, but based on a similar property of delayed negative feedback. Specifically, we consider a single-gene circuit with negative feedback with delay.
The basic idea has been put forward multiple times, notably by Julian Lewis in 2003 (Lewis, 2003), describing transcriptional delay.
Delayed negative feedback is familiar to anyone who has encountered a poorly designed hotel room thermostat. The thermostat will turn on the heater in response to cold temperatures, overheating the room beyond the set point before shutting off and letting it cool well below the target temperature before turning the heater back on. These types of overshoot dynamics are usually regarded as a problem to be eliminated by more sophisticated controller designs—a major goal of control theory.
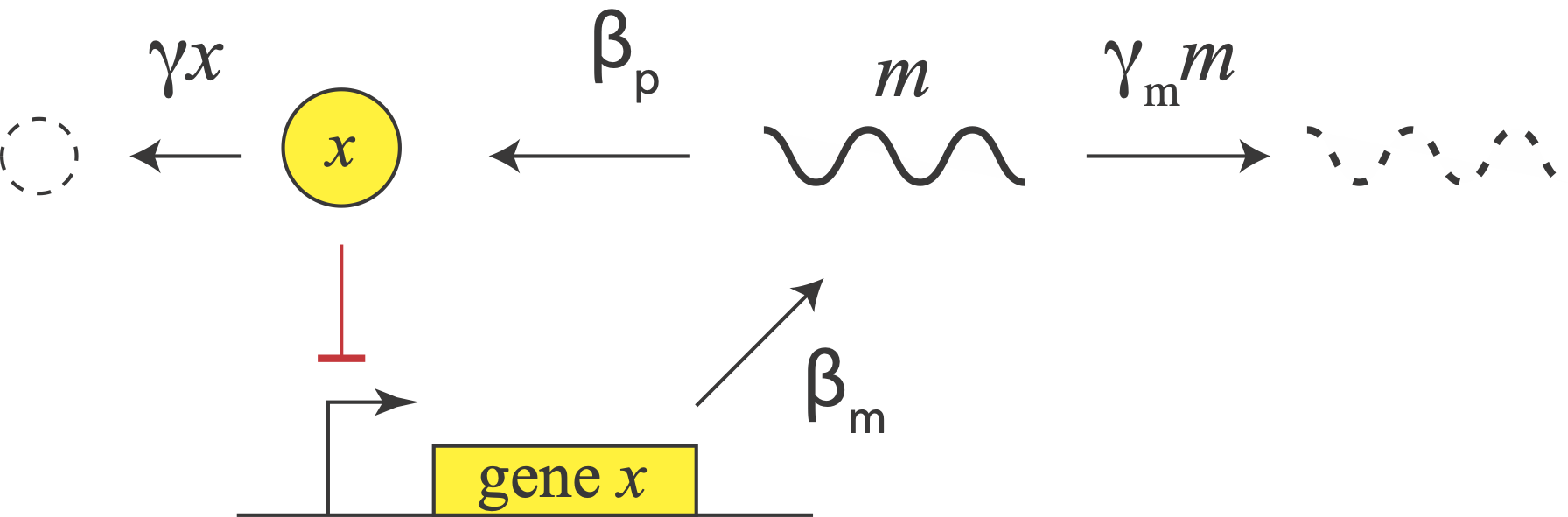
Let us consider a repressor that negatively autoregulates its own production, as in the above diagram. The concentration of the protein does not instantaneously reflect the expression level of its own gene. There is delay due to the transcription and translation steps we have already encountered. But there is also a second source of delay. The appearance of a freshly translated protein does not actually occur until translation is complete. That is, there is a delay between the initiation and completion of translation for each protein. (By contrast, translation can occur co-transcriptionally in bacteria, so translation does not have to wait to start before transcription is finished.)
In E. coli, translation occurs at a rate of about 15 amino acids per second. So a sizable protein like β-galactosidase can take more than a minute to translate.
In eukaryotic cells, where gene expression has additional steps, including splicing and nuclear export, these delays can be even longer. In fact, a totally different synthetic single gene negative autoregulation oscillator circuit was implemented in eukaryotic cells using the variability in intron length (Swinburne, et al., 2008), rather than translational delay per se, to delay protein production.
An example of delay in a biological circuit
To investigate how molecular details can give rise to delay (which in turn can give oscillations), we consider a multistep process of the production and action of a repressor. The delay in transcriptional regulation in real cells comes from processes such as translation, trans-nuclear transport, protein folding, dimerization, etc. We will consider a simple version of this, shown below, in which rᵢ is some intermediate state en route to functioning protein, and there are \(N\) such intermediates. For simplicity, we will assume the rate constants for moving from mRNA to the first intermediate and for moving from intermediate to intermediate are all the same.

We can write the dynamics as
\begin{align} &\frac{\mathrm{d}m}{\mathrm{d}t} = \frac{\beta_{m}}{1 + (p/k)^n} - \gamma_m m,\\[1em] &\frac{\mathrm{d}r_1}{\mathrm{d}t} = k_{r} m - k_{r} r_1,\\[1em] &\frac{\mathrm{d}r_i}{\mathrm{d}t} = k_{r} r_{i-1} - k_{r} r_i\; \text{for } 2 \le i \le N,\\[1em] &\frac{\mathrm{d}p}{\mathrm{d}t} = k_{p} r_N - \gamma_{p} p, \end{align}
where for simplicity we have assumed mass action type kinetics for all processes other than expression of mRNA under repression by the protein p. These equations can be nondimensionalized by redefining variables as \(t \leftarrow \gamma_m t\), \(p \leftarrow p/k\), \(m \leftarrow k\gamma_pm/k_p\), and \(r_i \leftarrow k\gamma_pr_i/k_p\), and defining dimensionless parameters \(\beta = \beta_{m} k_p/k\gamma_m\gamma_p\), \(\gamma = \gamma_p/\gamma_m\), and \(\kappa = k_r/\gamma_m\) to give
\begin{align} &\frac{\mathrm{d}m}{\mathrm{d}t} = \frac{\beta}{1 + p^n} - m,\\[1em] \kappa^{-1}\,&\frac{\mathrm{d}r_1}{\mathrm{d}t} = m - r_i,\\[1em] \kappa^{-1}\,&\frac{\mathrm{d}r_i}{\mathrm{d}t} = r_{i-1} - r_i\; \text{for } 2 \le i \le N,\\[1em] \gamma^{-1}\,&\frac{\mathrm{d}p}{\mathrm{d}t} = r_N - p. \end{align}
There is a single fixed point \((m_0, r_{1,0}, \ldots, r_{N,0}, p_0)\) for this system,
\begin{align} m_0 = r_{1,0} = \cdots = r_{N,0} = p_0, \end{align}
with
\begin{align} \beta = m_0(1+m_0^n). \end{align}
We perform linear stability analysis about this fixed point in Technical Appendices 10a and 10b. As laid out in the technical appendices, we can prove that ultrasensitive repression is necessary to get an instability and that any instability is oscillatory. However, we cannot solve for the eigenvalues analytically, as we have done in previous examples. We instead take a “brute force” approach and grid up parameter space and compute the eigenvalues for each set of parameter values and determine if that point is stable or not. We can then display the linear stability diagram as an image, where a pixel is light colored in a stable region and dark colored in an unstable region. The result is shown below.
[2]:
from IPython.display import HTML
HTML(filename="figs/delay_cascade_lin_stab.html")
[2]: